APPENDIX A.A
Mandelbar Variation Snowflakes
Mandelbar Variation Snowflakes use Mandelbrot variations, actually Mandelbar variations.
Mandelbrot is (x+iy)² and Mandelbar is (x-iy)² which produces a three-pronged figure.
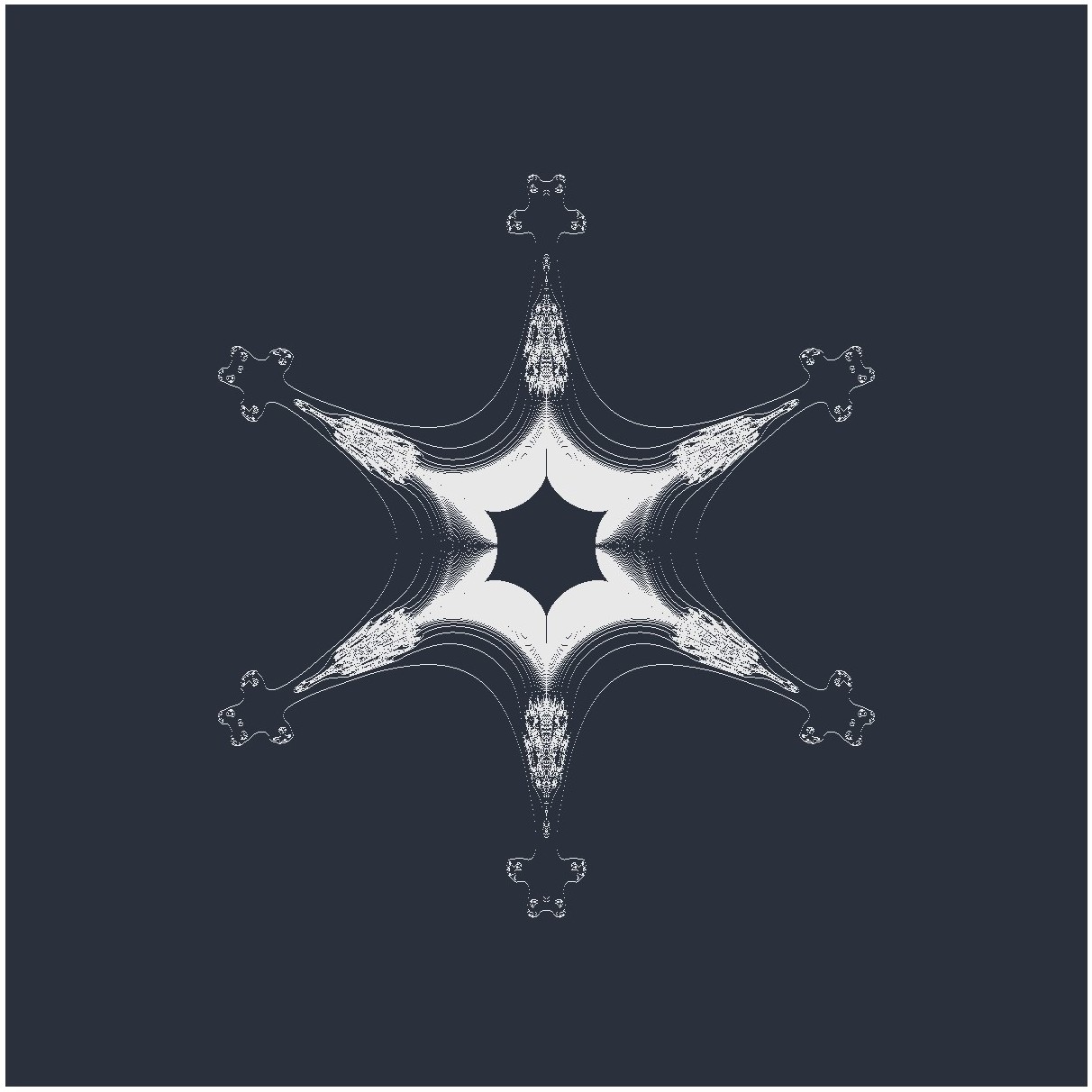
The expression (x-iy)⁵ produces a six-pronged figure with the figure not quite radially symmetric, but with a snowflake shape.
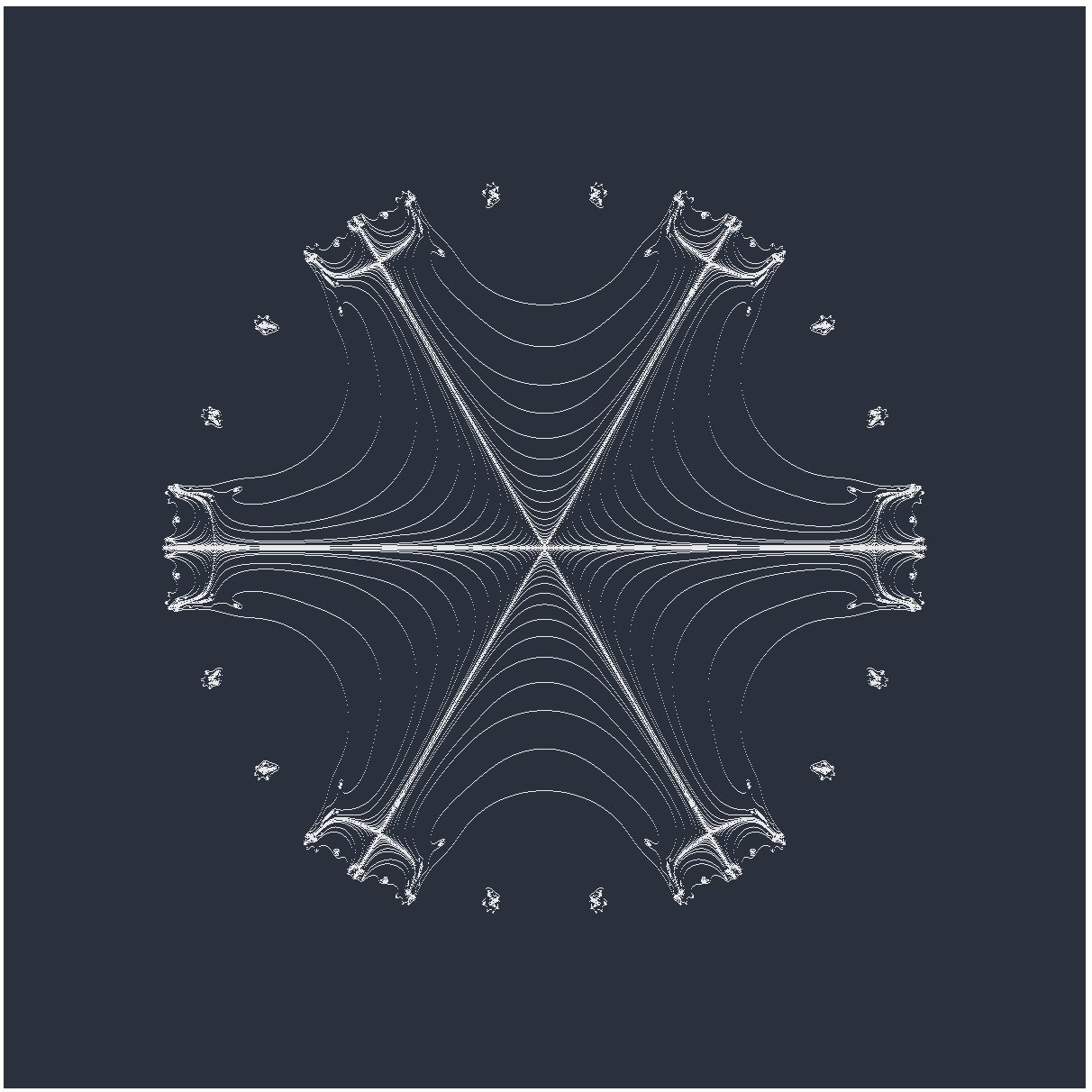
 Six-Pronged Mandelbar Expanded Center
Six-Pronged Mandelbar Expanded Center
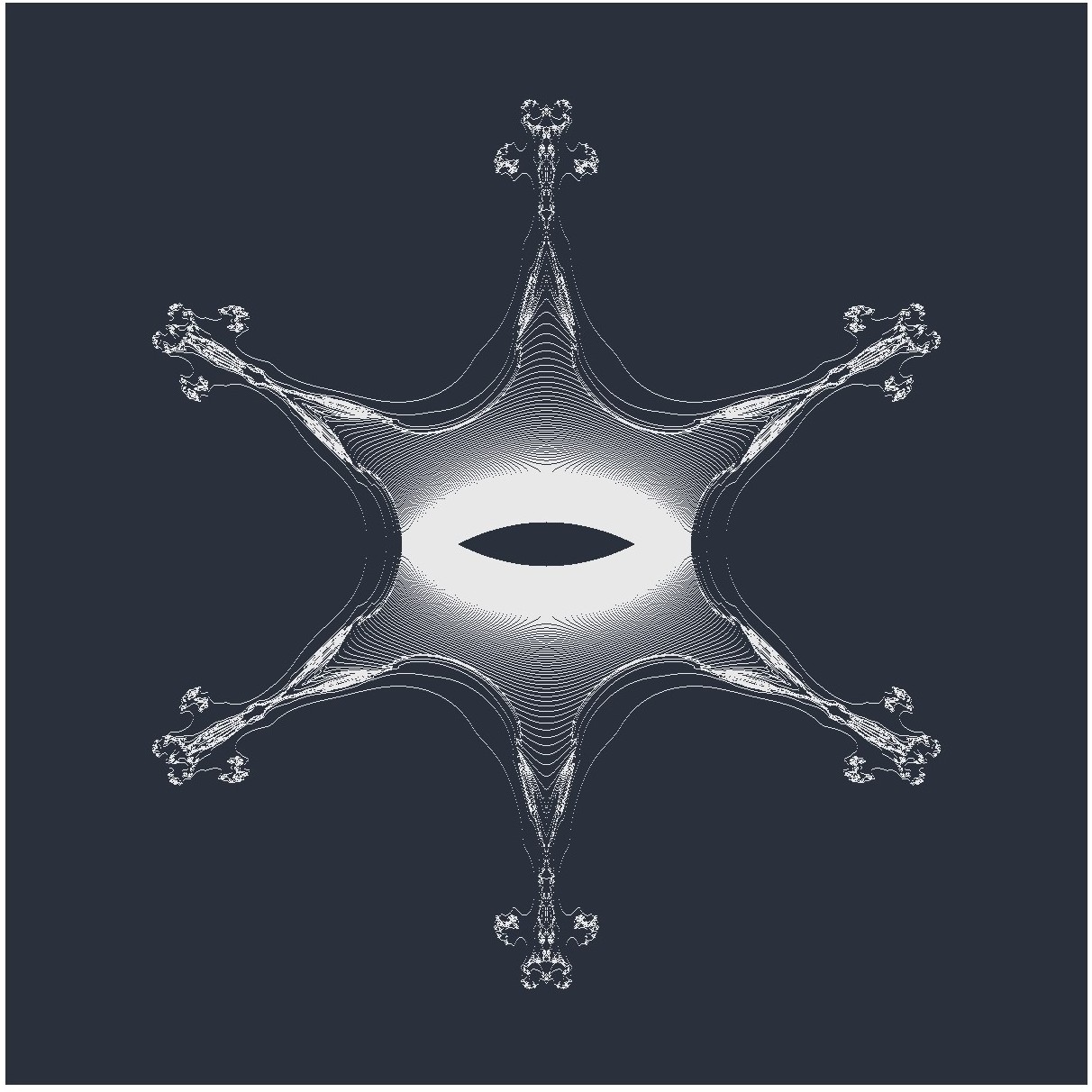
 Six-Pronged Mandelbar Snowflake
Six-Pronged Mandelbar Snowflake

for (i = 0; i ≤ 800; i++)
{
for (j = 0; j ≤ 800; j++)
{
x = 0.0;
y = 0.0;
xs = -4.0+(i / 100.0);
ys = -4.0+(j / 100.0);
k = 0;
do
{
k = k+1;
xnew = x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
x = xnew;
y = ynew;
} while ((k ≤ 255) && (x*x+y*y ≤ 16.0));
PlotPixel(i, j, color);
}
}
Six-Pronged Mandelbar Expanded Center with PseudocodeThe center of the Six-Pronged Mandelbar is expanded to reveal the prongs.
for (i = 0; i ≤ 1200; i++)
{
for (j = 0; j ≤ 1200; j++)
{
x = 0.0;
y = 0.0;
xs = -1.5+(i / 400.0);
ys = -1.5+(j / 400.0);
k = 0;
do
{
k = k+1;
xnew = x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
x = xnew;
y = ynew;
} while ((k ≤ 255) && (x*x+y*y ≤ 16.0));
PlotPixel(i, j, color);
}
}
Six-Pronged Mandelbar Snowflake with PseudocodeTo obtain this figure, pixels are plotted at iteration count increment.
for (i = 0; i ≤ 1200; i++)
{
oldk = 0;
for (j = 0; j ≤ 1200; j++)
{
x = 0.0;
y = 0.0;
xs = -1.5+(i / 400.0);
ys = -1.5+(j / 400.0);
k = 0;
do
{
k = k+1;
xnew = x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
x = xnew;
y = ynew;
} while ((k ≤ 255) && (x*x+y*y ≤ 16.0));
if ((oldk != k) && (k > 3) && (oldk > 3)) PlotPixel(i, j, color);
oldk = k;
}
}
| Snowflake | Build: (f(x,y), g(x,y)) | Escape: h(x,y)>value |
|---|---|---|
| Example | (x⁵-10.0*x³*y²+5.0*x*y⁴, -y⁵+10.0*x²*y³-5.0*x⁴*y) | x²+y²>16.0 |
| Snowflake #1 | (x⁵-10.0*x³*y²+5.0*x*y⁴-0.125*x, -y⁵+10.0*x²*y³-5.0*x⁴*y-0.125*y) | x²+y²>16.0 |
| Snowflake #2 | (x⁵*k-10.0*x³*y²*k+5.0*x*y⁴*k, -y⁵*k+10.0*x²*y³*k-5.0*x⁴*y*k) | x²+y²>16.0 |
| Snowflake #3 | (x⁵-10.0*x³*y²+5.0*x*y⁴, -y⁵+10.0*x²*y³-5.0*x⁴*y) | x²+y²>16.0/k |
| Snowflake #4 | (x⁵-10.0*x³*y²+5.0*x*y⁴, -y⁵+10.0*x²*y³-5.0*x⁴*y) | |x|>16.0/k |
| Snowflake #5 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x, -y⁵+10.0*x²*y³-5.0*x⁴*y-y) | |x|+|y|>16.0/k |
| Snowflake #6 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/k, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/k) | |x|+|y|>16.0/k |
| Snowflake #7 | (x⁵*k-10.0*x³*y²*k+5.0*x*y⁴*k+x/k, -y⁵*k+10.0*x²*y³*k-5.0*x⁴*y*k+y/k) | x²+y²>16.0 |
| Snowflake #8 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/3.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/3.0) | x²+y²>16.0/k |
| Snowflake #9 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x*1.25, -y⁵+10.0*x²*y³-5.0*x⁴*y-y*1.25) | x²+y²>16.0/k |
| Snowflake #10 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/2.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/2.0) | x²+y²>16.0/k |
| Snowflake #11 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x/10.0, -y⁵+10.0*x²*y³-5.0*x⁴*y-y/10.0) | x²+y²>16.0/k |
| Snowflake #12 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/20.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/20.0) | x²+y²+|x|+|y|>16.0/k |
| Snowflake #13 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x/20.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/4.0) | x²+y²+|x|>16.0/k |
| Snowflake #14 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/k, -y⁵+10.0*x²*y³-5.0*x⁴*y)+y/k) | x²+|y|>16.0/k |
| Snowflake #15 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/k, -y⁵+10.0*x²*y³-5.0*x⁴*y)+y/k) | |y|>16.0/k |
| Snowflake #16 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/k, -y⁵+10.0*x²*y³-5.0*x⁴*y)+y/k) | |x|>16.0/k |
| Snowflake #17 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x/2.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y/2.0) | |x|>16.0/k |
| Snowflake #18 | (x⁵-10.0*x³*y²+5.0*x*y⁴+x*k/12.0, -y⁵+10.0*x²*y³-5.0*x⁴*y+y*k/12.0) | |x|>16.0/k |
| Snowflake #19 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x*k/12.0, -y⁵+10.0*x²*y³-5.0*x⁴*y-y*k/12.0) | |x|>16.0/k |
| Snowflake #20 | (x⁵*k-10.0*x³*y²*k+5.0*x*y⁴*k-x/k, -y⁵*k+10.0*x²*y³*k-5.0*x⁴*y*k-y/k) | |x|>16.0/k |
| Snowflake #21 | (x⁵*k-10.0*x³*y²*k+5.0*x*y⁴*k-x/k³, -y⁵*k+10.0*x²*y³*k-5.0*x⁴*y*k-y/k³) | |x*y²|>16.0/k |
| Snowflake #22 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x/k, -y⁵+10.0*x²*y³-5.0*x⁴*y -y/k) | x²+y²>16.0/k |
| Snowflake #23 | (x⁵-10.0*x³*y²+5.0*x*y⁴-x/k², -y⁵+10.0*x²*y³-5.0*x⁴*y-y/k²) | x²+y²+|x|+|y|>16.0/k |
| Snowflake #24 | (x⁵/k-10.0*x³*y²/k+5.0*x*y⁴/k-x/k³, -y⁵/k+10.0*x²*y³/k-5.0*x⁴*y/k-y/k²) | x²*y²*|x|*|y|+|x|>16.0/k |





















 FRACTAL FIND
FRACTAL FIND