Fractal Feigenbaum Example

Introduction to Fractal Feigenbaum Sets

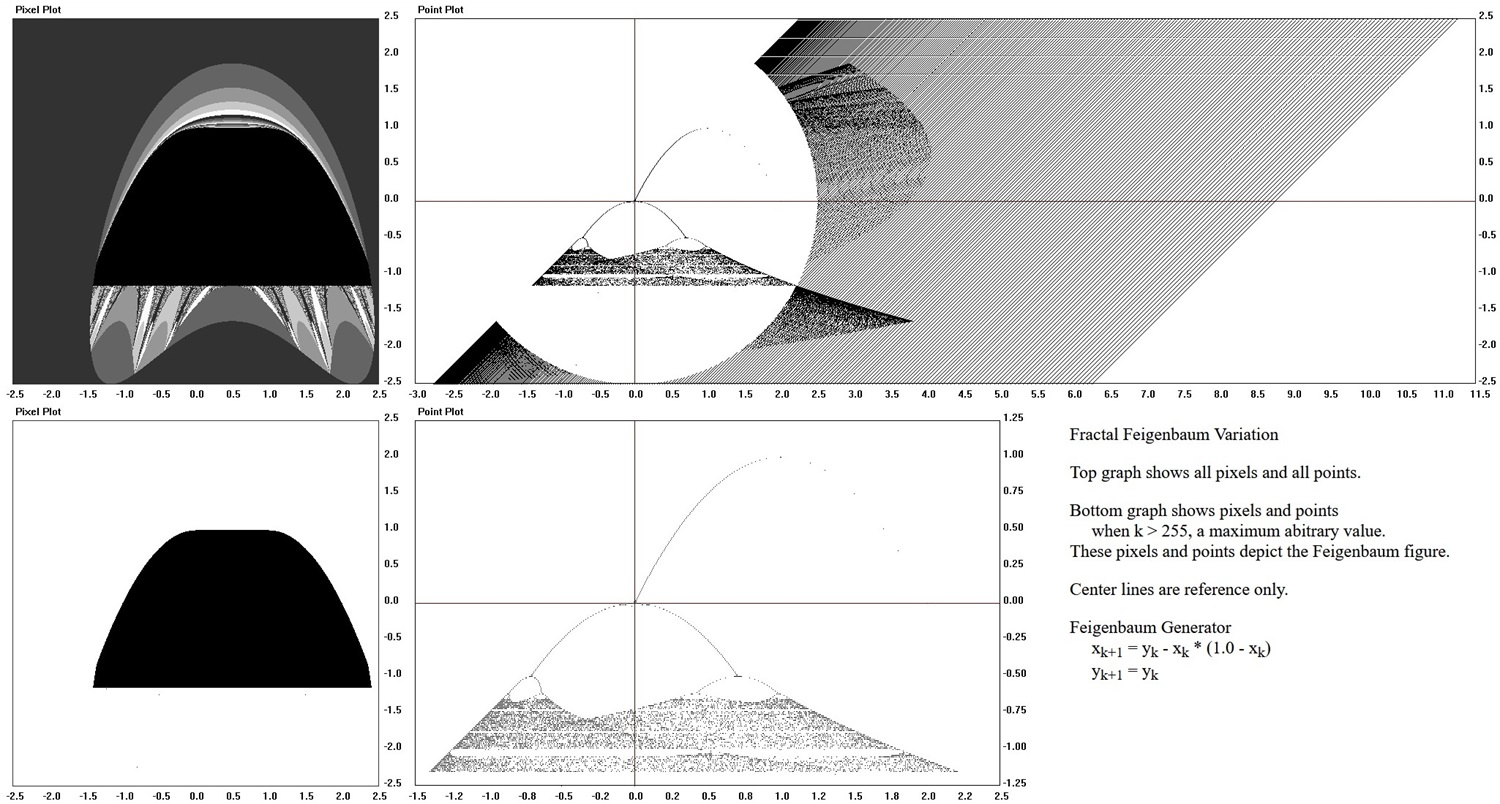
Fractal Feigenbaum sets are built with Julia set structure.

Feigenbaum computation may be shown as x_k+1 = a * x_k * (1.0 - x_k)

If the Feigenbaum computation is treated as part of the Julia x_k+1 calculation and y_k+1 = y_k,
then a Feigenbaum figure is generated when the count, k, exceeds an arbritrary maximum value, k_max.

Feigenbaum Julia Set with Pseudocode

for (int i = 0; i ≤ 500; i++)
{
	for (int j = 0; j ≤ 500; j++)
	{
		xs = 0.0;
		ys = 0.0;
		x = -2.5 + (i / 100.0);
		y = -2.5 + (j / 100.0);
		k = 0;
	        do
		{
			k = k + 1;
			xnew = y - x * (1.0 - x) + xs;
			ynew = y + ys;
			x = xnew;
			y = ynew;
		} while ((k ≤ 255) && (x * x + y * y ≤ 6.25));
		PlotPixel(i, j, color);
		PlotPoint(x*scale, y*scale, color);
		if (k > 255) PlotPixel(i, j, color);
		if (k > 255) PlotPoint(x*scale, y*scale, color);
   	 }
}

See Appendix J for additional Feigenbaum figures.