APPENDIX J
Fractal Feigenbaum Figures
Fractal Feigenbaum Figures use Julia variations where:
- xnew = f(y + (x * (1.0 - x)))
- ynew = y or -y
- c = (xs, ys)
- k = iteration count
Example Fractal Feigenbaum with Pseudocode
Feigenbaum Example
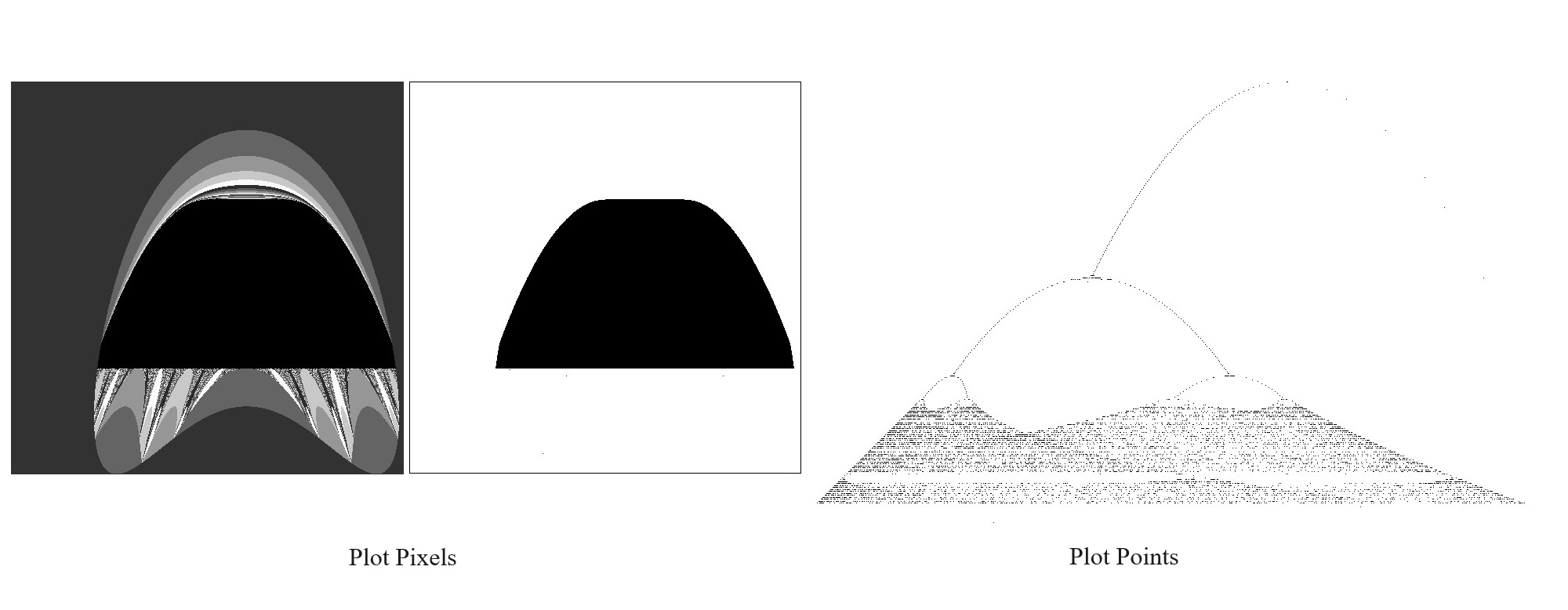

for (int i = 0; i ≤ 500; i++)
{
for (int j = 0; j ≤ 500; j++)
{
xs = 0.0;
ys = 0.0;
x = -2.5 + (i / 100.0);
y = -2.5 + (j / 100.0);
k = 0;
do
{
k = k + 1;
xnew = y - x*(1.0-x) + xs;
ynew = y + ys;
x = xnew;
y = ynew;
} while ((k ≤ 255) && (x*x + y*y ≤ 6.25));
PlotPixel(i, j, color);
if (k > 255) PlotPixel(i, j, color);
if (k > 255) PlotPoint(x*scale, y*scale, color);
}
}
| Feigenbaum | Build: (f(x,y), g(x,y), c) | Escape: h(x,y)>value |
|---|---|---|
| Example | (y - x * (1.0 - x), y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #1 | (-y - x * (1.0 - x), y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #2 | (y + x - x * x * x, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #3 | (y * y + x - x * x * x, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #4 | (x * y - x + x * x + y, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #5 | (x * y - x + x * x + y - y / k, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #6 | (y + x - x * x * y, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #7 | (y * y - x * (1.0 - x * y) , y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #8 | (y * y * y - x * (1.0 - x), y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #9 | (y - x * (1.0 - 2.0 * x), y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #10 | (-y - x * (1.0 + x), -y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #11 | (y * y + x - x * x, y, (0.0, 0.0)) | x²+y²>6.25 |
| Feigenbaum #12 | (-x * y - x + x * x + y, y, (0.0, 0.0)) | x²+y²>6.25 |
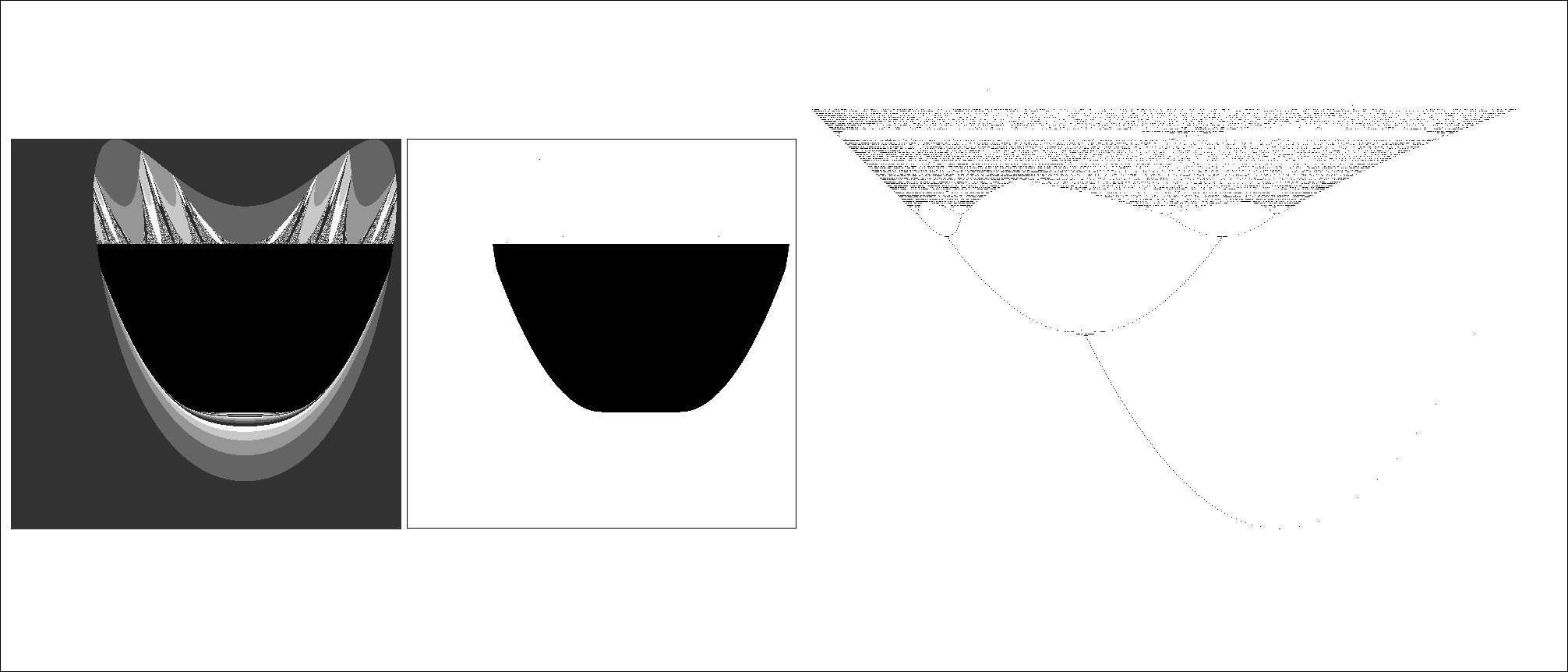



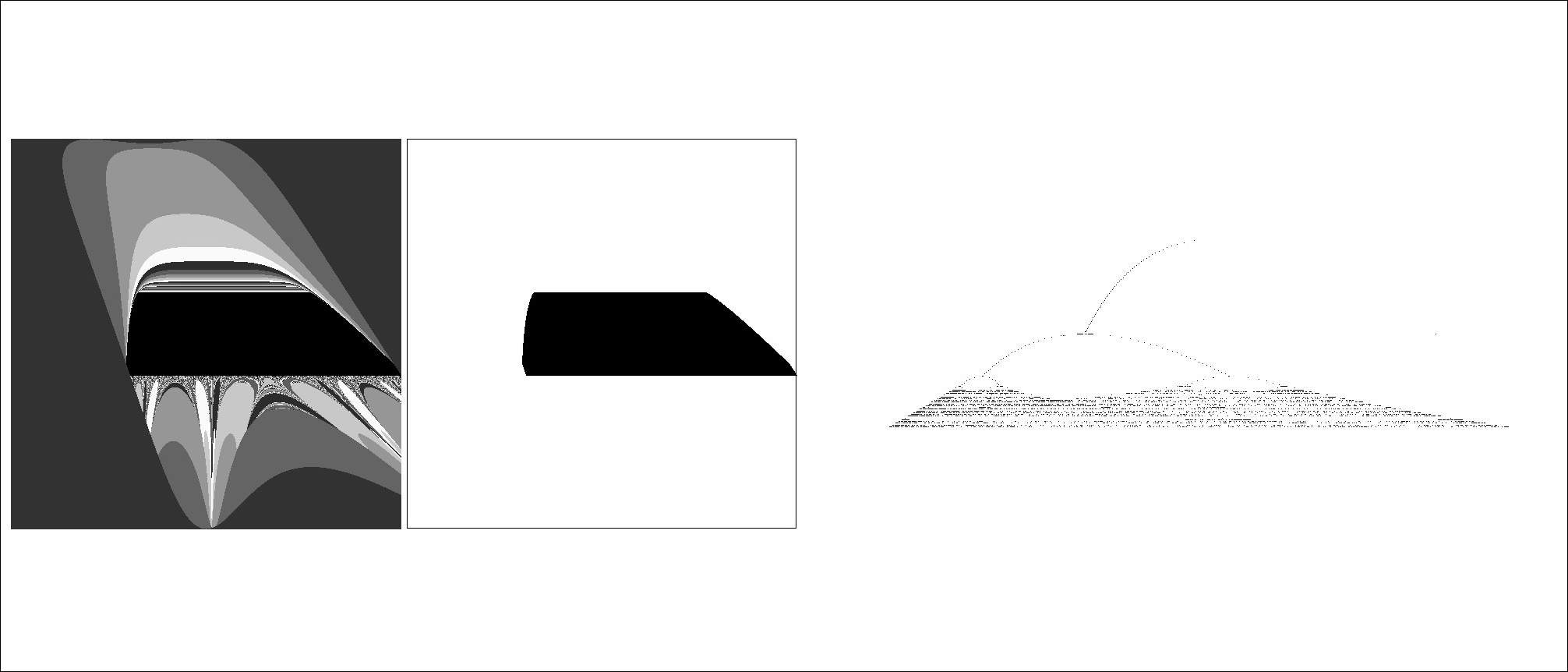
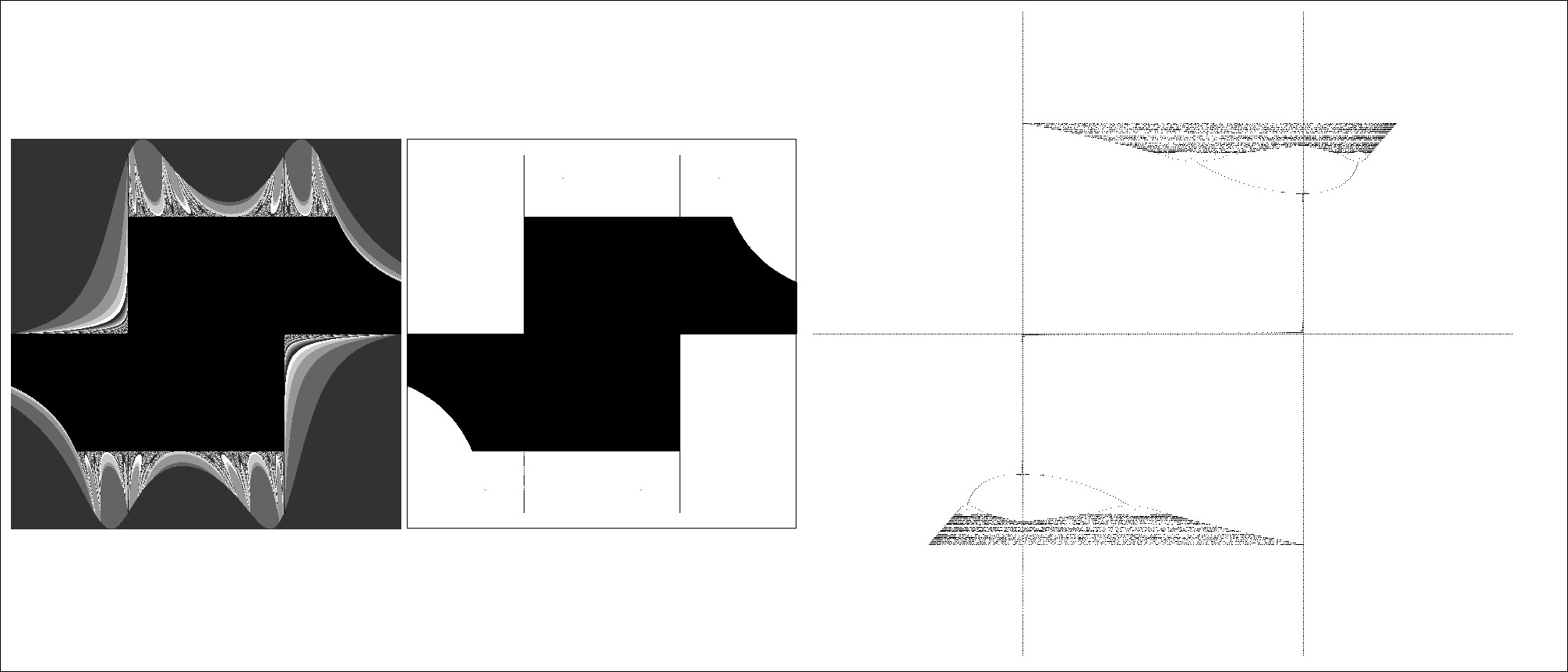




 FRACTAL FIND
FRACTAL FIND